Sep 16, 2021

Log-Structured Merge-Tree

简介

LSM-Tree 的设计可以认为受两个观点的启发：

  • The Five Minute Rule ：对于硬盘中的结构，当存在相对热的硬盘页时， 引入内存结构来分摊硬盘 I/O 开销 。
  • Log-Structured ：对于写场景较多的硬盘中的结构， 使用日志结构，转化随机写为顺序批量写来降低写入硬盘 I/O 开销 。

LSM-Tree 是针对 写多读少 的场景提出的，在这个场景下，经典的 B-tree 的写放大会导致额外的 I/O 开销：

Unfortunately, standard disk-based index structures such as the B-tree will effectively double the I/O cost of the transaction to maintain an index such as this in real time, increasing the total system cost up to fifty percent.

LSM-Tree 是一种硬盘上的数据结构，能在多写且建索引的场景下降低 I/O 开销：

The Log-Structured Merge-tree (LSM-tree) is a disk-based data structure designed to provide low-cost indexing for a file experiencing a high rate of record inserts (and deletes) over an extended period.

LSM-Tree 的核心思想是 延迟且批量化顺序化写操作 ： 先将写入缓存到内存中的结构，积攒够后用类似归并排序的思路级联地 merge 到一个或多个硬盘中的结构。

The LSM-tree uses an algorithm that defers and batches index changes, cascading the changes from a memory-based component through one or more disk components in an efficient manner reminiscent of merge sort.

此外，为了最小化 I/O 代价，LSM-Tree 提出了磁盘中的分层结构。

对于写操作，LSM-Tree 的写操作直接在内存中进行，然后 dump 到硬盘，将对硬盘的随机写转化为连续写，相比 B-Tree 减少了磁盘臂的移动。

对于读操作，LSM-Tree 会导致读放大，导致硬盘 I/O 压力增大。

  • 但是基于局部性原理 ，大部分读应该能在内存的结构中完成。

相比维护 B-Tree，维护 LSM-Tree 的优势在于 Log-Structured ，并以 Multi-Page Block 写入，这带来的好处是：

  • 写入以 Batch 的形式，使得每个对象的写入开销被均摊
  • 维护结构的 Rolling Merge 是顺序读顺序写

关键结构

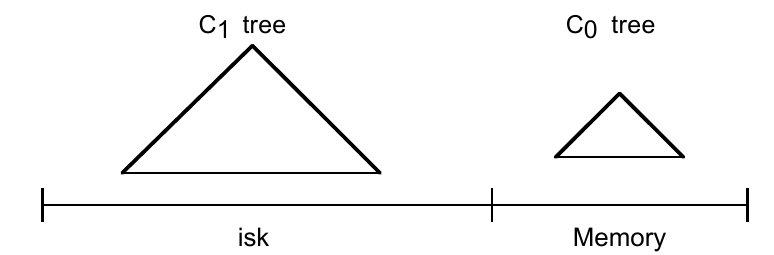
先从引入内存结构考虑，我们有 The Two Component LSM-Tree ，即内存中的 \(C_0\) 和硬盘中的 \(C_1\) 。

  • \(C_0\) 由于在内存中，结构可以比较自由
  • \(C_1\) 和 B-Tree 类似，但是做了顺序硬盘访问优化，以优化 rolling merge 阶段。
    • 节点全满
    • root 节点是单页的
    • 对于深度相同的非 root 的单页节点，被存放在一个硬盘块的连续页中
    • 在 merge 阶段进行 multi-page block I/O

由 n+1 个相似的结构组成，1 个存储在内存， n 个存储在硬盘（由于页缓存，热页可能会放在内存中，有内存缓存的页可以认为存储在内存）。

关键过程

插入

  1. 插入到 \(C_0\) 中，
  2. 当 \(C_0\) 大小达到阈值时，触发向 \(C_1\) 的 rolling merge ，即从 \(C_0\) 中删除一段连续的元素，并将这些元素 merge 进 \(C_1\) 。

更新

  1. 同插入

删除

  1. 同插入，但是是追加写一个删除标记。

查找

  1. 先查找 \(C_0\) ，再查找 \(C_1\)
  2. 查找 \(C_1\) 时的访问是 single-page 的。

Rolling Merge

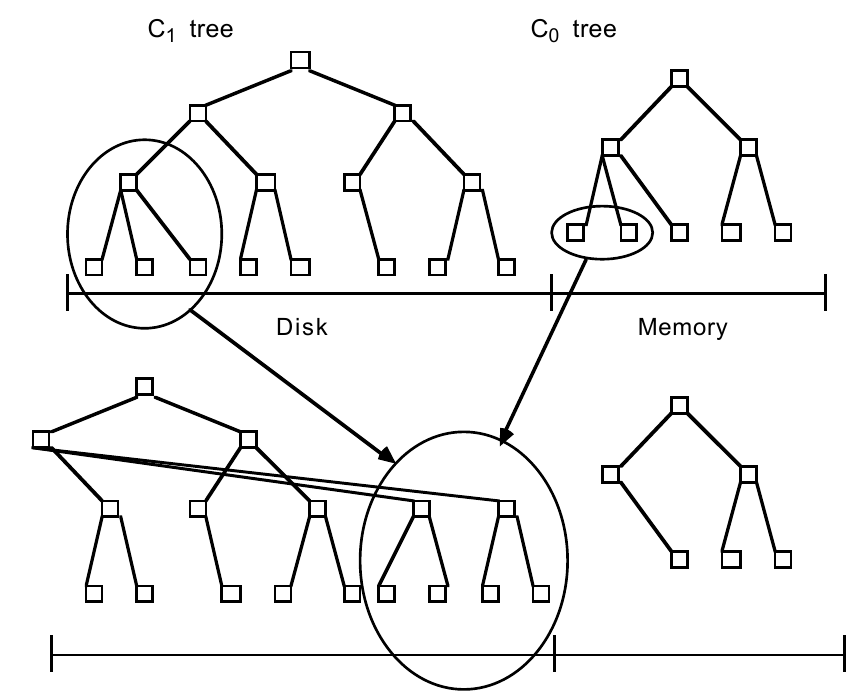
当 \(C_0\) 的大小达到阈值时，需要进行 rolling merge ，过程为：

  • 维护 \(C_0\) 中的迭代器 \(i\) 和 \(C_1\) 中的迭代器 \(j\) ，初始时在各自序列的起始处。
  • 读取一个 emptying block （存放 \(C_1\) 叶节点的 multi-page block ），使得一段从迭代器 \(i\) 开始的连续的 \(C_1\) 元素缓存在内存中
  • 不断循环进行以下操作：
    • 从迭代器 \(j\) 开始读取一页 \(C_1\) 元素
    • 与对应区间的 \(C_0\) 元素对进行 merge ，并更新迭代器 \(i\) 和迭代器 \(j\) ，若 \(i\) \(j\) 达到末尾则从头开始，这就是所谓的 rolling 。
    • 将结果写入 filling block （每一页是一个存放 merge 结果的 \(C_1\) 叶节点），这个 block 紧挨着 \(C_1\) 末尾的页节点所在的 block 。

细节：

  • rolling emerge 是尽可能 multi-page 的，将一个 block 视为一个 buffer ，只有写入页填满这个 block 才真正写入。
  • \(C_1\) 同层节点的写入的地址是递增且相邻的，除非：
    • block buffer 已满，需要新分配 block
    • 根节点分裂，导致深度变化
    • 设置 checkpoint
  • 这里的 filling block 不会写到 emptying block 中，这样可以比较方便地做故障恢复。但是当 rolling merge 完成后，emptying block 可以被回收
  • \(C_1\) 的非叶子节点页会被缓存，以待更新

故障恢复

显然，LSM-Tree 只有内存结构是非持久化的，我们想要容错，只需要使用 WAL 保留内存结构的状态，并在 Rolling Merge 时使用额外的文件描述磁盘结构的状态及 Rolling Merge 的游标即可。

Two-Component LSM-Tree 分析

I/O 开销

假设：

\(COST_d\)
1MByte 磁盘的开销
\(COST_m\)
1MByte 内存的开销
\(COST_p\)
1 秒 1 次随机访问某个 page 的 I/O 开销
\(COST_\pi\)
1 秒 1 次通过 multi-page block I/O 访问某个 page 的 I/O 开销
\(S\)
数据总量，单位 MByte
\(H\)
一秒一次访问 H 个 page

则有：

\(H*COST_p\)
磁头开销
\(S*COST_d\)
容量开销

当不考虑引入内存减小 I/O 开销时，一般瓶颈为磁盘容量和磁盘访问速度中的一个，可以认为 I/O 开销为：

\(COST_D=max(H*COST_p,S*COST_d)\)

这是关于 H 和 S 的函数：

  • \(H/S\) 较小时：函数值由 \(S*COST_d\) 决定。
  • \(H/S\) 较大时：函数值由 \(H*COST_p\) 决定。

当 H/S 足够大，基于 The Five Minute Rule 可以考虑引入内存结构。

当考虑引入内存减小 I/O 开销时，对于被内存缓存的那部分硬盘页，则可以认为 I/O 开销为：

\(COST_{TOT}=min(COST_D,S*COST_m+S*COST_d)\)

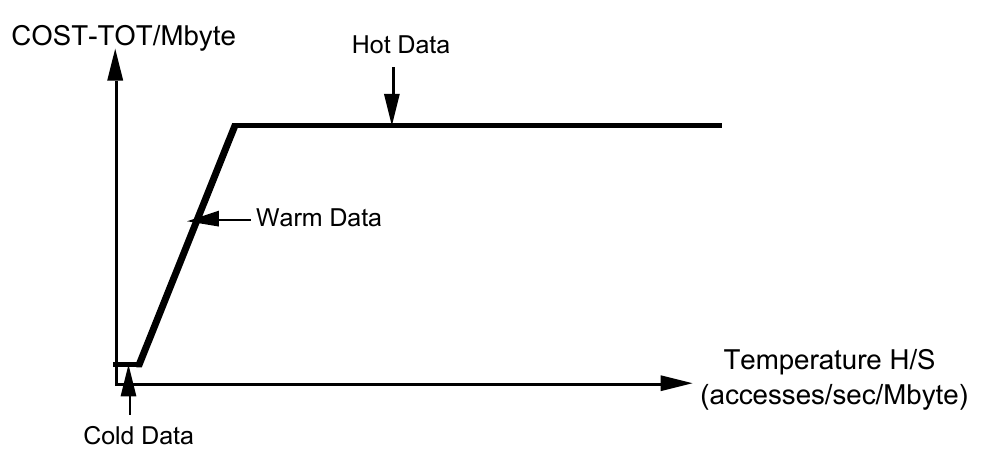
定义 \(H/S\) 为 数据热度（the temperature of a body of data） ，可见 \(H/S\) 在值域上可分为三个区间，存在两个拐点：

Cold Data
冷数据硬盘存储，此时公式由 \(S*COST_d\) 决定。
T_f
\(COST_d/COST_p\) , temperature division point between cold and warm data (“freezing”)
Warm Data
数据较热瓶颈在硬盘 I/O 开销，此时公式由 \(H*COST_p\) 决定
T_b
\(COSTm/COSTp\) , temperature division point between warm and hot data (“boiling”)
Hot Data
热数据内存存储，此时公式由 \(S*COSTm\) 决定

引入 multi-page block I/O 后，即可以理解为用 \(COST_\pi\) 替换 $COST_p$，而 \(COST_\pi\) 可以认为比 \(COST_p\) 小一个数量级，即十分之一。这样做之后，上面函数的 \(T_f\) 和 \(T_b\) 都大大增大，同时拉长整个函数，可见 multi-page block I/O 收益可观，让原本需要考虑引入内存结构的热数据访问，变为只需要进行硬盘 I/O 的冷数据访问。

B-Tree 开销

平均一个 entry 的写入开销：

\(COSTb_{ins}=COST_p*(Depth+1)\)

LSM-Tree 开销

假设：

\(S_e\)
entry size
\(S_p\)
page size
\(S_0\)
size of C0 component leaf level
\(S_1\)
size of C1 component leaf level
\(S_p / S_e\)
the number of entities to a page

则 M —— 在 rolling merge 过程中，\(C_0\) merge 到 \(C_1\) 的一个 page leaf node 中的平均的来自 \(C_0\) 的 entry 数为： \(M=(S_p/S_e)*(S_0/(S_0+S_1))\) 。

那么，\(C_0\) 写入一个 entry 会导致 \(C_1\) 写入 \((S_0+S_1)/S_0\) 个 entry 。

而 rolling merge 中需要先读后写，则平均一个 entry 的写入开销为： \(COST_{lsm-ins}=2*COST_\pi/M\)

B-Tree 开销对比 LSM-Tree 开销

将两者做比，得到 \(K_1*(COST_\pi/COST_p)*(1/M)\) ，即：

  • multi-page block batch size 影响 \(COST_\pi/COST_p\)
  • \(S_0/S_1\) 影响 \(1/M\)

恰好和 LSM-Tree 的优点对应，multi-page block batch size 越大 LSM-Tree 越优，内存结构占比越大约优。

Multi-Component LSM-Tree

根据上文，若 \(M\) 太小， LSM-Tree 性能不如 B-Tree ，而 \(M\) 又由 \(S_0/S_1\) 决定。

  • 若 \(S_0\) 太小，会频繁触发 rolling merge
  • 若 \(S_0\) 太大，内存开销巨大

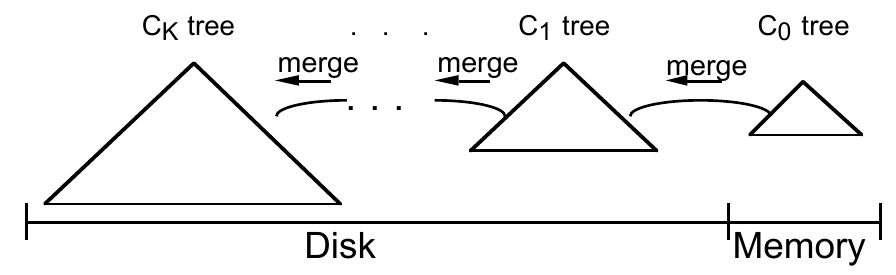
若我们在维持 \(S_0\) 较小的前提下引入 multi-component ，使得原本的 \(S_1\) 变为 \(S_n\) ， \(S_1\) 到 \(S_k\) 逐步递增，则我们既减小了内存开销，又使得 \(M\) 变大，减少每次写导致的写扩散，减少硬盘 I/O 开销。

Multi-Component LSM-Tree 分析

对于 Multi-Component 我们定义

假设：

  1. 以每秒 \(R\) 字节的速度向 \(C_0\) 写
  2. 除 \(C_k\) 外，其余每一级 Component 都已达到 Threshold
  3. \(C_k\) 的大小相对稳定

定义：

  • \(r_i\) 为相邻两级 Component 的 threshold 比例
  • \(S_i\) 为第 \(i\) 级 Component 大小，那么总大小为 \(S=\sum_0^k S_i\) 。
  • \(S_p\) 为一 page 的字节大小

那么我们有：

Given an LSM-tree of k+1 components, with a fixed largest-component size Sk, insert rate R, and memory component size S0, the total page I/O rate H to perform all merges is minimized when the ratios ri = Si/Si-1 are all equal to a common value r.

亦即当所有 \(S_i/(S_i+1)\) 相等时，开销最小，此时：

\(S=S_0+rS_0+r^2S_0+…+r^kS_0\) \(H=(2R/S_p)(K(1+r)-1⁄2)\)

假设 \(C_0\) 以 \(R\) 速率写入，对于极端情况下（不产生 merge），若各级以相同速率 \(R\) rolling merge ，则整体考虑开销，对于组分 \(C_{i-1}\) 以速率 \(R\) 读出，对于组分 \(C_i\) 以速率 \(r_iR\) 读出并以速率 \((1+r_i)R\) 写出，则总的 I/O 开销为：

\(H=(R/S_p)((2r_1+1)+(2r_2+2)+…+(2r_{k-1}+2)+(2r_k+2))\) （因为 \(C_0\) 是内存结构，所以可以省去一个 \(R\)）

即：

\(H=(2R/S_p)(\sum\limits_{i=1}^{K}r_{i} + k + \frac{1}{2}))\)

且满足约束：

\(\prod\limits_{1}^{K}r_{i} = (Sk / S0) = C\)

则由算术——几何平均数的不等式易证极值条件。

TODO C 的选取，层级选取，写放大的分析等

实现

  • LevelDB

参考资料